[概要] 計算機で扱う問題は,多くの場合グラフ上の問題として定式化できる. 計算量の理論により,これまで多くの問題が``手に負えない''ことが示されてきた. 一方でこうした問題に対する現実的なアプローチがいくつか提案されてきた. 本稿ではグラフに制限を加えるアプローチについて解説する.DNA の切片間の関係などは, モデル化すると特別なグラフになる.こうしたグラフ上では, これまで手に負えないとされてきた問題が効率良く解けることがある. 本稿では,代表的なグラフクラスと,関連したアルゴリズムの最近の研究動向を解説する.
[キーワード] アルゴリズム,グラフクラス,計算の複雑さ,理想グラフ
[お断り] このページは,電子情報通信学会に掲載予定の同名の解説論文を加筆修正したものです. せっかく書いたので,より広く公開して,かつ,ときどきは更新して行こうかと思っています. リンクも少しずつ充実させるつもりです. (最終変更日:2005年1月1日)
ここでは,さまざまなグラフのクラスと,これに関連したアルゴリズムの研究動向を解説する. ``グラフのアルゴリズム''と言っても,もちろん「表計算ソフトで棒グラフや円グラフを描く方法」 といった話ではない. 世の中の森羅万象を頂点と呼ばれる``点''と辺と呼ばれる``線''を使ってモデル化する, 数学で言う所のグラフである. 「グラフ理論なんて数学じゃない」と言う数学者も,最近はめっきり少なくなってきたので, 本稿で「数学で言う所のグラフ」と言っても差し支えなかろう.
さて,世の中の多くの問題は,グラフ上の問題として定式化できる. これまで,計算量の理論と呼ばれる分野では,こうしたグラフ上の問題の多くが, どんなに高速なコンピュータを使っても``手に負えない''問題であることを示してきた. 典型的な問題としては次の「ハミルトン路問題」が挙げられる.
ここでは各都市が頂点であり,二つの都市を結ぶ道が辺に該当する. 原理的には,候補となる経路をすべてチェックすれば答は必ず見つけることができる. 数学的には面白くもなんともない問題である. またコンピュータで単純にチェックを行なうプログラムを作るのも,簡単である. しかし,ちょっと都市の数が大きくなると,こうしたプログラムでは 現実的な時間で答を見つけることは不可能になる. この問題は計算量の理論ではNP完全問題と呼ばれており, どんなに工夫して高速化しても,都市の数が大きくなると, 一般には実際的な時間で答を見つけることはできない. これが計算量の理論における結論である.
理論的にダメだ,と言われて,そこであきらめることができるなら良いのだが, 現実問題としてはそうはいかない.そこで,さまざまな「現実的」な枠組みが提案され, 理論的に研究されてきた.特に最近では,
といった枠組みが活発に研究されている (もう一つ固定パラメータ容易性(Fixed Parameter Tractability)[DF99]という 無視できない枠組みがあるのだが,ここではあえて無視する).
本稿で紹介するのは,3つ目の枠組みである. つまり入力されるグラフに妥当な制限を加える,というアプローチである. 例えばハミルトン路問題であれば 「道の総数は都市の総数に比例する」とか 「ある都市につながっている道の数はせいぜい100本」といった制限は, ある程度の妥当性を持つ,自然な制限と言えるであろう. このように入力に制限をつけたときに,それを使うことによって, ``手に負えない''問題が``手に負える''問題になることがある.
では,どんなグラフが「妥当性を持っている」とされるのか, またどんな問題がそのグラフ上で解けるのか.本稿ではそのごくごく一部を概観したい.
本稿で扱っているグラフクラスとアルゴリズムに関する研究は,歴史的には1950年代後半に始まった,と言える. 当時,数学系の研究者である Hajösと, 分子生物学者である Benzer とが``区間グラフ''と呼ばれる グラフクラスを独立に考えたことに端を発している\cite[Chapter 8]{Gol04}. 区間グラフでは,各頂点は「数直線上のある区間」に対応する. そして二つの区間が重なっているとき,対応する二つの頂点は辺で結ばれる.
 |
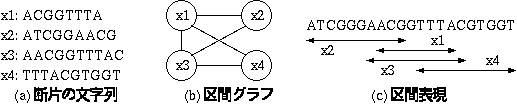
ここでまず区間グラフと分子生物学の関連について補足しておこう. 全ゲノムショットガン法と呼ばれる解析方法では,まずゲノムをたくさんの断片に分ける. そしてこれらの断片同士が「重なり」を持つかどうかという情報を使って元のゲノムの配列を構築する. この場合,ゲノムの断片を文字列上の区間ととらえれば,断片の情報を表すグラフは区間グラフとなる(図1). 例えば4つの断片x1,x2,x3,x4の重なりを調べた結果,x2とx4は重なりを持たないことがわかったとする. このときこの4つの断片を頂点とすると,対応する区間グラフ(b)が得られる. この区間グラフ(b)は(c)に示した区間表現を持つ.
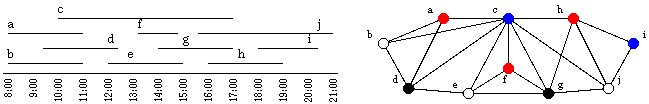
|
区間グラフは実生活の中でもよく見られるグラフである. 例えば工程表の例を考えてみよう(図2). 各仕事ごとに作業時間を割り当て(例えば仕事aは8:00〜11:00,仕事hは16:00〜19:00など), これを区間,すなわちグラフの頂点と見なすのである. この場合,区間グラフの頂点はそれぞれの仕事に対応し, 例えば頂点aと頂点bの間に辺があるときは(これらは時間が重なるので),一人の人間は 仕事aと仕事bを担当することができない,ということになる.
こうした工程表を実行するにあたり,作業員は最低何人いれば足りるのであろうか. ある頂点集合Cを見たとき,どの二つの頂点間も辺で結ばれているなら, Cをクリーク(clique)と呼ぶ. このとき,すぐに次のことがわかる: 『グラフがクリークCを含むなら,最低でも|C|人の作業員が必要である.』 (|C|はクリークCに含まれる頂点の数を表す.)
つまり,工程表に対応する区間グラフが与えられたとき,最大のクリークを求めれば, 少なくともそれだけの人数は必要であることはわかる. 実は区間グラフではこうした最大のクリークの大きさは簡単に求めることができる. 図2の工程表であれば,各時刻に『いくつの仕事が同時に行なわれているのか』を 順番に見ていけばよい. すると{a,b,c,d}や{c,g,j,h}など,大きさ4のクリークがあることがわかる.
ではこの場合,4人いれば十分なのであろうか.もし4人で十分であれば, 元の区間グラフを『どの辺の両側も色が違う』ように4色で塗り分けることができるはずである. このように『どの辺の両側も色が違う』ような塗り分けに必要な,最小の色の数を彩色数と呼ぶ. 実は区間グラフでは,最大のクリークの大きさと彩色数が一致することがわかっている. 図2の工程表では例えば図にあるように{a,f,h}, {b,e,j}, {c,i}, {d,g}と塗り分ければよい. つまり,これらの仕事の集合にそれぞれ担当する作業員を割り当てることにすれば, 図2の工程をこなすには4人いれば十分であることがわかる.
| 図3:最大クリークの大きさは2で,彩色数は4のグラフ:もしこれが工程表なら, 一見2人で仕事がこなせそうなのに,実際には4人いないと仕事がこなせない. | 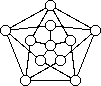 |
なお,一般のグラフでは「最大のクリークの大きさ」よりも「彩色数」の方が大きくなる. 図3のグラフは,最大クリークの大きさは2であるが,塗り分けには4色必要である. つまり図3のグラフは区間グラフではない.
このように区間グラフは日常さまざまな場所で現れるが,有用な性質を多数持っていため, 従来は手に負えなかったさまざまな問題を簡単に解くことができる. 例えばハミルトン路問題も簡単に解くことができる[Dam93]. 昨今では特にDNA関連の問題が,区間グラフモデルや, さらにそれを一般化したグラフモデル[Ueh04]の上で考えられ, 研究されている.
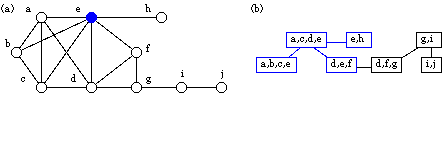
頂点が循環的につながっている場合,例えば頂点v1,v2,v3, v4,v5が それぞれ辺{v1,v2}, {v2,v3}, {v3,v4}, {v4,v5}, {v5,v1}でつながっている場合,これをサイクルと呼ぶ. 区間グラフ上で長さ4のサイクル (v1,v2,v3,v4,v1)を考えると, どんな区間表現を考えても,{v1,v3}か, あるいは{v2,v4}が辺となる. こうした「サイクル上にあり,かつサイクルを構成しない辺」のことを弦と呼ぶ. 弦グラフ(chordal graph)とは, 「長さ4以上のサイクルは必ず弦を持つ」という特徴を持つグラフである(図4(a)).
|
弦グラフは,1970年代にさまざまな分野で独立に考えられたグラフクラスである. そのため,弦グラフ(chordal graph)以外にも,triangulated graph, rigid circuit graph などと呼ばれていて,どの呼び名を使うかで, その人の出身や年代がわかる([Gol04]のEpilogue 2004).
弦グラフはこうしたサイクルを用いた定義以外にも,いくつかの同等な定義があることが知られている. 特に美しいのは,次の定義である. まず木Tを考える.なお,木とはサイクルを含まない連結なグラフのことである. 各頂点vはそれぞれ,Tの部分木Tv, つまりTの一部の頂点からなる小さな木Tvに対応する. そして頂点uと頂点vは,対応する部分木TuとTvが 同じ頂点を含むときに辺で結ばれる. (これは区間グラフの一般化にもなっている.つまり区間グラフは弦グラフである.) 例えば図4(a)の弦グラフに対応する木Tの一例が図4(b)である. 木の頂点Nの中に弦グラフの頂点vが書かれているとき, 頂点Nは部分木Tvに含まれていることを意味している. 例として図4(a)の弦グラフの頂点eに対応する部分木Teを青で示した.
この定義は単に美しいだけではなく,アルゴリズムを構成する上で有用な,多くの性質をもつ. 特に木Tのそれぞれの頂点は,元の弦グラフの極大クリークと 1対1で対応づけることができる. (より正確には,そうなるようにTを作ることができる.) そのためこの木Tをクリーク木と呼ぶ. 図4(b)の木は,クリーク木の一つである. このクリーク木から,図4(a)の弦グラフの極大クリークは7つあり, 最大クリークは大きさ4のものが2つあることがわかる. そしてそれらは具体的に{a,b,c,e}と{a,c,d,e}の2つであることもわかる.
一方,弦グラフは,頂点の順序付けで定義されることもある. ある頂点vと,その隣接点の集合N(v)が,グラフ上でクリークになっているとき, その頂点をsimplicialである,と言う. また与えられたグラフGに対して,一部の頂点を取り出し, Gの辺をそのまま引き継いで構成したグラフを導出部分グラフと呼ぶ. 頂点の並びv1,v2,…,vnが 「各頂点viは{vi,vi+1,…,vn}に 導出されるグラフ上でsimplicialである」 という条件を満たすとき(条件を満たす並びがあったとき), そのグラフは弦グラフであり,その並びのことを perfect elimination orderingと呼ぶ. 例えば図4(a)の弦グラフであれば, j, i, h, g, f, d, e, c, b, a は perfect elimination ordering である. 一般に perfect elimination ordering はいくつもある. 例えば図4(a)の弦グラフの j, i, h, g, f, d, e, c, b, a という順序づけについて, j と h の順番を入れ換えたり,e,c,b,a の順番を入れ換えても,やはり perfect elimination ordering であることがわかる.
与えられたグラフが弦グラフであるかどうかを判定するアルゴリズムは, 1970年代にいくつか提案された. 特に Rose, Tarjan, Lueker によって文献[RTL76]で提案されたアルゴリズムは LexBFS (Lexicographically Breadth First Search;辞書式順序に基づいた幅優先探索)と呼ばれ, 名前は複雑だが,アルゴリズム自体は非常に単純で,かつ高速に動作する. 実装も本当にやさしい. LexBFS は与えられたグラフが弦グラフのときは,perfect elimination ordering を出力する. 1990年代には,この perfect elimination ordering からクリーク木を構築する, 単純かつ高速なアルゴリズムもいくつか示されている[Spi03]. (なお LexBFS そのものも,いろいろなグラフクラスの認識に使える, ということで最近一部で熱心に研究されている[Cor04].)
これらの多彩な特徴づけを使うと,弦グラフ上ではいろいろな問題を効率良く解くことができる. 例えば最大のクリーク,最大の独立点集合(互いに辺で結ばれていない頂点集合), 彩色数などが簡単に求めることができる[Gav72]. 一方ではハミルトン路問題は弦グラフ上でもNP困難であり, 依然として手に負えない問題であることも知られている[Mul96].
つまり同じ``手に負えない''問題であっても,どのグラフクラスで簡単になるのか, という境界線は,問題によって(かなり)違ってくるのである. この境界線を明確にする,ということは, とりも直さずその問題の「どこが本質的に難しいのか?」という点を 明確にすることにもつながる.
すでに見たように,一般のグラフでは,最大クリークの大きさは彩色数よりも小さい. しかし理想グラフ(perfect graph)と呼ばれているグラフでは,この二つが一致する. より正確に言えば,理想グラフとは『すべての導出部分グラフにおいて 最大クリークの大きさと彩色数が一致するグラフ』のことである. 定義がかなりわかりにくいが,区間グラフも弦グラフも理想グラフのごく一部を占めているにすぎない. 理想グラフとは,これらを含むかなり大きなグラフの集合である.
理想グラフ上では,彩色数や最大クリークの大きさ, 最大独立点集合などを効率良く見つけることができる. これらの問題は,代表的なNP完全問題であり,``手に負えない''問題である. こうした問題が効率良く解けるという,好ましい性質と, グラフのクラスが集合として大きいという性質とから,理想グラフは幅広く研究されてきた.
理想グラフの定義は上で示した通りなのであるが, 実はもっと単純な特徴づけとわかりやすい定義があるのではないか,という予想が 40年以上も前から言われていた.1960年に Berge は 『あるグラフGが理想グラフである』ということと, 『Gとco(G)とが, 長さが5以上の奇数長の「弦を持たないサイクル」を導出部分グラフとして持たない』 ということが同値である,と予想した. (co(G)はGの辺の有無を反転したもので,補グラフと呼ばれる.) これは「強理想グラフ予想」と呼ばれて,いた. そして2002年5月に「強理想グラフ予想」は「強理想グラフ定理」と呼ばれるようになった. Chudnovsky, Seymour, Robertson, Thomas らが強理想グラフ予想の証明に成功したのである (詳細は[Chv03]に詳しい).
この結果により,今後は理想グラフの定義,あるいは性質として「強理想グラフ定理」が使えるようになった. この性質は,もともとの定義や特徴付けに比べるとずっと単純であり,直観的にもわかりやすい. そのため,アルゴリズムを構成するときの「入力グラフが満たす性質」としても使いやすいように思う. 今後は,もっと多くの``手に負えない''問題が,理想グラフという大きなグラフクラス上で, 実際的な時間で解けるようになることが期待できる.
本稿で紹介したグラフのクラスは,どちらかと言えばグラフ理論からのアプローチである. そのため,グラフの性質をいわば静的に定義してきた. これとはやや趣が異なるアプローチとして,グラフをある条件の下でランダムに生成する, というモデルもある.これは1960年代に提案された Random Graph という概念がその始まりであり, 特に1980年代以降,活発に研究された分野である. 通常 Random Graph と言ったときは,各辺が確率pで独立に存在するというモデルを使うことが多い. このため,生成されるグラフは一様な構造となる[Bol01].
近年 WWW に代表されるインターネット上のサービスは,私たちの日常に深く入り込んでいる. しかしインターネットのネットワーク構造は,Random Graph のような一様性を持っているようには とても見えない.筆者の使っている貧弱な端末と,日本の基幹となるDNSサーバとでは, ネットワークへの接続の``太さ''はまったく違っている.
もう少し具体的に言うと,インターネットをモデル化するグラフでは, 一部の少数の頂点には辺が集中し,多数の頂点にはそれほど辺が集中していない, という性質を持っていなければ,説得力がない. こうした『ごく一部に接続が集中する』という現象をうまく説明できるモデルとして, 近年 Power Law と呼ばれる法則が注目を集めている. (これはベキ法則,ベキ乗則などと訳されている.) こうした Power Law を満たすグラフを確率的に生成する方法も提案されている.
こうした``Web Graph''の理論的な研究は,Webの普及とともに1990年代後半にはじまったばかりである. しかし目ざとい研究者たちが,最近ではかなり精力的に研究を行なっている. ([BKMRRSTW00]などが参考になる.) この分野も非常にエキサイティングな分野ではないか,と筆者は注目している.
グラフ理論については,和書,洋書ともに最近は優れた教科書がいくつもある. しかし,あるグラフのクラスが「なぜ導入されたのか?」「どういう問題に使えるのか?」という 素朴な疑問に答えるものはそれほど多くはない.文献[ET97]は, それぞれのグラフクラスについて, こうした疑問に答えてくれる例が豊富に示されているので,初学者には読みやすい. また,計算量の理論についても優れた教科書がいくつもあるが, 初学者にも読みやすい,という点で文献[Iwa03]を推す. この文献は最新の結果もさりげなく採り入れていて,例えば「固定パラメータ容易性」という 概念を日本語でいち早く紹介しているのは,筆者が知る限りではこの本だけである.
本稿で扱った内容を詳しく紹介している文献としては文献[Gol04]が挙げられる. 1980年に刊行された同書の初版は,この分野の『教科書』として有名であった. 今回の改定版では,その後の20年間における進展もかなり取り込まれているし, 代表的な文献を紹介している点でも推薦できる.
文献[BLS99]は, 本稿で紹介しているグラフクラスの分野がどれほどの広がりを持つのかを把握するには, 欠かせない.この本は「読む」本というよりは,関連文献を「調べる」ための本と言える. 300ページほどの分量中に,紹介されているグラフクラスが160個あまり, 参照されている論文数が1100本以上である. 論文リストを軽く眺めるだけでも,1990年以降にこの分野がいかに活発に研究されてきたかがよくわかる.
文献[Gol04]と文献[BLS99]との 中間的な本として文献[Spi03]も挙げておく. 最後の方を読むと「今どんな問題が研究されているのか?」という最前線の情報が得られる.
|
Last modified: Mon Jan 10 22:45:14 JST 2005
by R.Uehara (uehara@jaist.ac.jp) |