


Next: Calculation of physical parameters
Up: Wavelet filterbank with the
Previous: Characteristic of the gammatone
To represent the wavelet transform as Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ), we will
redesign the gammatone filter by the Hilbert transform.
As a results, basic wavelet becomes
), we will
redesign the gammatone filter by the Hilbert transform.
As a results, basic wavelet becomes
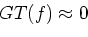 |
(15) |
wavelet filterbank is designed with a center frequency
f0 of 600 Hz, a bandpassed region from 60 Hz to 6000 Hz, and
a number of filters K of 128.
For convenience, we have used the integral (continuous) wavelet
transform; however, when the wavelet filterbank is implemented on a
computer, we will use a discrete wavelet transform with the following
conditions[18]:
sampling frequency fs=20 kHz, the scale parameter
 ,
and the shift
parameter b=q/fs, where
,
and the shift
parameter b=q/fs, where
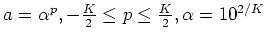 .
Frequency characteristics of the wavelet filterbank are shown in Fig.
.
Frequency characteristics of the wavelet filterbank are shown in Fig.
![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
Amplitude characteristics of this filterbank overlap completely with
the bandpassed region as shown in Fig.
.
Amplitude characteristics of this filterbank overlap completely with
the bandpassed region as shown in Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) while ERB
(Equivalent Rectangular Bandwidth) of the filters are do not
[18].
while ERB
(Equivalent Rectangular Bandwidth) of the filters are do not
[18].
Masashi Unoki
2000-10-26