Graph Catalogs
In this page, we provide graph catalogs of the following graph classes:
The list provides all
nonisomorphic connected chain graphs of n vertices for n=1,2,...,24.
The numbers of graphs are summarized as follows
Each line contains a sequence of degrees of one of bipartite set.
That is, the number of chain graphs of 4 vertices is three
and they are given by [1,1,1], [2,1], and [2,2] as follows: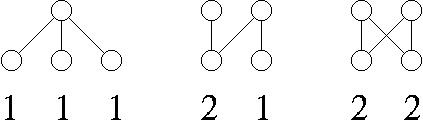
The list provides all nonisomorphic caterpillars of n vertices for n=1,2,...,24.
The numbers of graphs are summarized as follows
Each line contains a sequence of degrees of the backbone of
a caterpillar. We note that we assume that the endpoints of
the backbone has one leaf as a default, and these leaves are not counted.
That is, the number of caterpillars of 5 vertices is three
and they are given by [0,0,0], [0,1], and [2] as follows:
The lists provide
all nonisomorphic distance hereditary graphs of n vertices for n=1,2,...,14.
The numbers of graphs are summarized as follows
Each distance hereditary graph is represented in the following form:
n m
list of edges.
For example, the set of distance hereditary graphs of three vertices is
descirbed as
3 2
0 1
0 2
3 3
0 1
0 2
1 2
The first graph has 3 vertices with 2 edges {0,1} and {0,2}, and
The second graph has 3 vertices with 3 edges {0,1} and {0,2}, and {1,2}.
The lists provide
all nonisomorphic Ptolemaic graphs of n vertices for n=1,2,...,15.
The numbers of graphs are summarized as follows
Each Ptolemaic graph is represented in the following form:
n m
list of edges.
For example, the set of distance hereditary graphs of three vertices is
descirbed as
3 2
0 1
0 2
3 3
0 1
0 2
1 2
The first graph has 3 vertices with 2 edges {0,1} and {0,2}, and
The second graph has 3 vertices with 3 edges {0,1} and {0,2}, and {1,2}.
(As same as the set of distance hereditary graphs up to there.
Please remind that the set of Ptolemaic graphs is the intersection of
the sets of chordal graphs and distance hereditary graphs.)
The lists provide
all nonisomorphic interval graphs of n vertices for n=1,2,...,14.
The numbers of graphs are summarized as follows
Each interval graph is represented in one line in a simple text format, e.g.,
1 1 2 2 3 3 (independent set of three vertices),
1 2 1 3 2 3 (path of length 3),
1 2 3 3 2 1 (complete graph of size 3).
The lists provide all nonisomorphic permutation graphs of n vertices for each of n=1,2,...,8.
The numbers of graphs are summarized as follows
| The number of vertices |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
The number of permutation graphs |
1 |
2 |
4 |
11 |
33 |
142 |
776 |
5699 |
The number of connected permutation graphs |
1 |
1 |
2 |
6 |
20 |
99 |
600 |
4753 |
Each permutation graph represented in one line in a simple text format, e.g.,
1 2 3 (independent set of three vertices),
2 3 1 (path of length 3),
3 2 1 (complete graph of size 3).
The list provides all nonisomorphic proper interval graphs of n vertices for n=1,2,...,23.
The numbers of graphs are summarized as follows
Each interval graph is represented in one line in a simple text format, e.g.,
[[[]]] (complete graph of size 3), [[][]] (path of length 3).
Histrory
- 2020/11/09: Update
-
Chain graphs (n=1,2,...,24)
(Thanks to Kazuaki Yamazaki.)
- 2020/11/04: Update
-
Caterpillars (n=1,2,...,24)
(Thanks to Kazuaki Yamazaki.)
- 2020/07/06: Update
-
Ptolemaic graphs (n=1,2,...,15)
(Thanks to Kazuaki Yamazaki.)
- 2020/06/12: Update
-
Distance hereditary graphs (n=13,14)
(Thanks to Kazuaki Yamazaki.)
- 2020/06/10: Update
-
Distance hereditary graphs (n=1,2,...,12)
(Thanks to Kazuaki Yamazaki.)
- 2019/09/04: Update & Bug fix
- Permutation graphs (n≤8)
- Connected permutation graphs (n≤8)
(Thanks to Kazuaki Yamazaki.)
- 2019/04/01-04/11: Update;
- Connected proper interval graphs (n=21,22,23)
(Special thanks to Prof. Ryuichi SAKAI at
Osaka Electro-Communication University.
He made a nice program for enumeration of these graphs.
Note that his program can compute for n=24, 25, but they
are too huge to put on the Web site.)
- 2019/03/19: Update;
- Connected proper interval graphs (n=19,20)
(Special thanks to Prof. Ryuichi SAKAI at
Osaka Electro-Communication University.
He made a nice program for enumeration of these graphs.)
- 2019/02/23: Update;
- Connected proper interval graphs (n=1,2,...,18)
- 2019/01/09: Update;
- We add the note about bugs for permutation graphs.
(Many thanks to Prof. Yota Otachi.)
- 2017/10/16: Update;
- Interval graphs (n=12)
- Connected interval graphs (n=12)
- 2017/08/24: Update;
- Interval graphs (n=11)
- Connected interval graphs (n=11)
- 2017/08/08: Update;
- Interval graphs (n=10)
- Connected interval graphs (n=10)
- 2017/07/20: Update;
- Permutation graphs (n=6)
- Connected permutation graphs (n=6)
- 2017/06/30: Open for the following graph classes;
- Interval graphs (n=1,...,9)
- Connected interval graphs (n=1,...,9)
- Permutation graphs (n=1,...,6)
- Connected permutation graphs (n=1,...,6)
Last modified: Fri Dec 24 20:14:43 JST 2010
by Ryuhei Uehara (uehara@jaist.ac.jp)
| 
|