[English/Japanese]

Nets which can be folded to 2 distinct boxes

This page gives you nets which can be folded to 2 distinct boxes. For example, see the following figure.

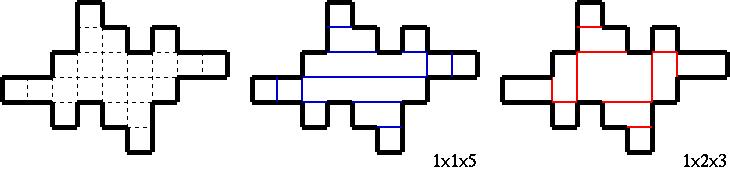
From the leftmost net, you can have a box of size 1x1x5 if you follow blue lines, but you can also have a box of size 1x2x3 if you follow red lines. The key point is that they have the same area and have different volumes. Two such nets can be found in Figure 25.53 in a recent great book "Geometric Folding Algorithms: Linkages, Origami, Polyhedra" (by Erik D. Demaine and Joseph O'Rourke). I was motivated by the figure, and I wonder if we have more such nets. Up to now, I found over 2000 such nets. (In August 2008, we found over 9000(!!) such nets. You can find further details in the long draft for CCCG 2008.)

I note that I presented this result at the following conferences. You can find more details by clicking the links.

Gathering for Gardner

I give a talk for this topic and distribute some puzzles at G4G9 on March 24-28, 2010 at Atlanta. You can see the patterns I distributed as puzzles here; PDF, EPS. They are quite nice puzzles to find two ways to fold. The real puzzles I distributed have guidelines for folding and some dimples so that they can keep in box-shape by themselves (see the right photo). Thanks to Tokyo-Shiki Co., Ltd, they are done by very fine process to make 1mm dimples and delicate cutlines.

4th Origami in Science, Mathematics, and Education (in Japanese; not 4OSME in US.)

June 22, 2008: The powerpoint file for the conference is here, but in Japanese.

The 20th Canadian Conference on Computational Geometry

August 13-15, 2008: The short version and the long version are now available.

In the following, I make lists of nets according to the size of area. Some nets are not valid in the following sense.

Corners are meeting.

I think this case is valid. See the following example.

Edges are meeting.

We have to cut an edge to make a box. I think this is invalid. In general, you have to cut different edges to make distinct boxes. This is not acceptable for me. Among the solutions, it might be a net that makes distinct boxes with cut the same edge. But I do not check that point. The following is the typical example.

Unit squares are overlapping.

A part of boxes are overlapping. In the following example, the area should be 22, but we have only 21 squares. That is, it has overlapping. Moreover, the overlapping areas are different according to the corresponding boxes. It is hard to say it is acceptable solution.

Actually, we can check such invalid nets from the algorithmic point of view. Precisely, we can check it in linear time as follows.

1. Count the number of boxes, and the net is invalid if the number is short.
2. Check if the net has a hole. We can check it by comparing the "area" in the net with the number of squares. After step 1, they should be equal if the net does not have a hole.

Area 22:

Valid nets: 538, Invalid nets: 18; All nets

[Add] On March 2011, Hiroaki Matsui, my student, succeed to enumerate all common developments of this case. To make a long story short, there are 2263 common developments that can fold to two boxes of size 1x1x5 and 1x2x3. Mr. Matsui is a great hitter. Here you can see all 2263 nets, but take care, it may be too large from foregn countries.

Area 30:

Valid nets: 72, Invalid nets: 1; All nets

Area 34:

Valid nets: 708, Invalid nets: 0; All nets

Area 38:

Valid nets: 41, Invalid nets: 0; All nets

Area 46:

Valid nets: 660, Invalid nets: 8; All nets

Area 54:

Valid nets: 3, Invalid nets: 0; All nets

Area 58:

Valid nets: 37, Invalid nets: 0; All nets

Area 62:

Valid nets: 5, Invalid nets: 0; All nets

Area 64:

Valid nets: 56, Invalid nets: 2; All nets

Area 70:

Valid nets: 14, Invalid nets: 0; All nets

Area 88:

Valid nets: 2, Invalid nets: 0; All nets

Total

Valid nets: :2139, Invalid nets: 26.

For each net, I have no data how to fold to 2 distinct boxes. Actually, they are interesting puzzles. Some nets are easy, but some nets are pretty difficult. So, have fun :-)

[Note] Dr. Tsuyoshi Ito had checked if there exists a net in the data above that can fold to 3 boxes or not by his program on 11 August, 2008. As a result, unfortunately, all nets above do not have the property. He also found that the number of invalid nets for the area size of 22 is 18, not 15. I thank him for his support.

Last modified: Thu Aug 21 13:49:33 JST 2008 by Ryuhei Uehara (uehara@jaist.ac.jp)