| = | (18) | ||
| = | (19) |
The system of the Kalman filtering is defined by
| (20) |
The minimum variance is sequentially calculated.
| (21) | |||
| (22) |
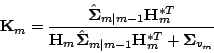 |
(23) |
| = | (24) | ||
| = | (25) |
| (26) |
In this paper, we reconsider how to estimate Ck,0 and Dk,0 from the observed component Xk(t) using Kalman filter.
The estimation duration is
[Th-1-Th].
It is then decomposed into discrete time
![]() ,
,
![]() ,
where the sampling period is
,
where the sampling period is
![]() and fs is the sampling
frequency.
and fs is the sampling
frequency.
First, Bk(t) and
![]() are estimated the Kalman filtering with the parameters in Eqs. (18) and (19) as shown in Table 2.
By performing the Kalman filtering according to Eqs. (18) and (19), we obtain the minimal-variance estimated value
are estimated the Kalman filtering with the parameters in Eqs. (18) and (19) as shown in Table 2.
By performing the Kalman filtering according to Eqs. (18) and (19), we obtain the minimal-variance estimated value
![]() and the covariance matrix
and the covariance matrix
![]() at discrete time tm.
Therefore, we obtain the estimated
at discrete time tm.
Therefore, we obtain the estimated
![]() and
and
![]() .
.
Next, we obtain the estimated
![]() and
and
![]() from Eqs. (4) and (6) from the above parameters.
from Eqs. (4) and (6) from the above parameters.
Finally,
Ck,0(t) and
Dk,0(t) are estimated with our previous Kalman filtering [Unoki and Akagi1999b] with the parameters in Eqs. (18) and (19) as shown in Table 2.
Note that let Ck(t) and Dk(t) be
![]() and
and
![]() ,
respectively.
By Performing the Kalman filtering according to Eqs. (18) and (19), we obtain the minimal-variance estimated value
,
respectively.
By Performing the Kalman filtering according to Eqs. (18) and (19), we obtain the minimal-variance estimated value
![]() and the covariance matrix
and the covariance matrix
![]() at discrete time tm.
As a result, the estimated
at discrete time tm.
As a result, the estimated
![]() and
and
![]() ,
and the estimated errors Pk(t) and Qk(t) are determined by
,
and the estimated errors Pk(t) and Qk(t) are determined by
![]() and
and
![]() ,
,
![]() ,
and
,
and
![]() ,
respectively.
,
respectively.