A Statistical Solution to Processing Very Large Datasets Efficiently with Memory Limit
Scientists develop a statistical randomness-based framework to optimally classify extremely large datasets without needing large memories
With the ever-increasing amount of data to process in a limited time-period, the required computational resources and corresponding expenses are likely to go up. To address this issue, scientists from Japan have developed a statistical framework that helps classify tremendously large datasets without requiring a memory boost or total sampling. The technique is widely applicable and can help sustain future high-speed computations even for sample sizes larger than the processing limit.
Any high-performance computing should be able to handle a vast amount of data in a short amount of time -- an important aspect on which entire fields (data science, Big Data) are based. Usually, the first step to managing a large amount of data is to either classify it based on well-defined attributes or--as is typical in machine learning--"cluster" them into groups such that data points in the same group are more similar to one another than to those in another group. However, for an extremely large dataset, which can have trillions of sample points, it is tedious to even group data points into a single cluster without huge memory requirements.
"The problem can be formulated as follows: Suppose we have a clustering tool that can process up to lmax samples. The tool classifies l (input) samples into M(l) groups (as output) based on some attributes. Let the actual number of samples be L and G = M(L) be the total number of attributes we want to find. The problem is that if L is much larger than lmax, we cannot determine G owing to limitations in memory capacity," explains Professor Ryo Maezono from the Japan Advanced Institute of Science and Technology (JAIST), who specializes in computational condensed matter theory.
Interestingly enough, very large sample sizes are common in materials science, where calculations involving atomic substitutions in a crystal structure often involve possibilities ranging in trillions! However, a mathematical theorem called "Polya's theorem," which utilizes the symmetry of the crystal, often simplifies the calculations to a great extent. Unfortunately, Polya's theorem only works for problems with symmetry and is, therefore, of limited scope.
In a recent study published in Advanced Theory and Simulations, a team of scientists led by Prof. Maezono and his colleague, Keishu Utimula, PhD in material science from JAIST (In 2020) and first author of the study, proposed an approach based on statistical randomness to identify G for sample sizes much larger (~ trillion) than lmax. The idea, essentially, is to pick a sample of size l that is much smaller than L, identify M(l) using machine learning "clustering," and repeat the process by varying l. As l increases, the estimated M(l) converges to M(L) or G, provided G is considerably smaller than lmax (which is almost always satisfied). However, this is still a computationally expensive strategy, because it is tricky to know exactly when convergence has been achieved.
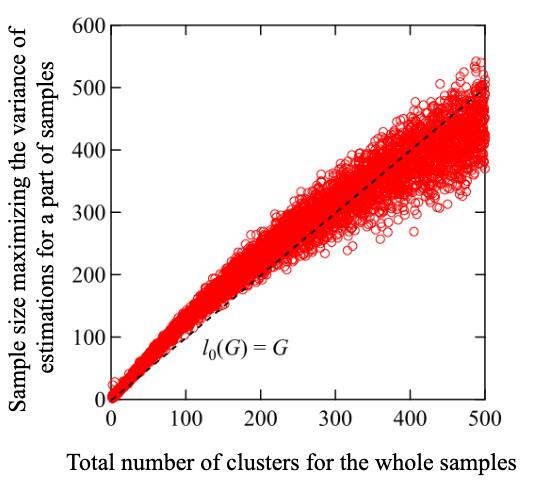
To address this issue, the scientists implemented another ingenious strategy: they made use of the "variance", or the degree of spread, in M(l). From simple mathematical reasoning, they showed that the variance of M(l), or V[M(l)], should have a peak for a sample size ~ G. In other words, the sample size corresponding to a maximum in V[M(l)] is approximately G! Furthermore, numerical simulations revealed that the peak variance itself scaled as 0.1 times G, and was thus a good estimate of G.
While the results are yet to be mathematically verified, the technique shows promise of finding applications in high-performance computing and machine learning. "The method described in our work has much wider applicability than Polya's theorem and can, therefore, handle a broader category of problems. Moreover, it only requires a machine learning clustering tool for sorting the data and does not require a large memory or whole sampling. This can make AI recognition technology feasible for larger data sizes even with small-scale recognition tools, which can improve their convenience and availability in the future," comments Prof. Maezono excitedly.
Sometimes, statistics is nothing short of magic, and this study proves that!
|
Figure: Plot of sample sizes at which the variance of the total number of attributes is the maximum. Estimating the variance of the number of clusters and the sample size for which it is maximum can give us an estimate of the total number of clusters for the whole sample. |
Reference
| Title of original paper: | Stochastic estimations of the total number of classes for a clustering having extremely large samples to be included in the clustering engine |
| Journal: | Advanced Theory and Simulations |
| DOI: | 10.1002/adts.202000301 |
Funding information
This study was funded by JAIST Research Grant (Fundamental Research) 2019, FLAGSHIP2020 (project numbers hp190169 and hp190167 at K-computer), KAKENHI grant (grant numbers 17K17762 and 19K05029), Grant-in-Aid for Scientific Research on Innovative Areas (16H06439 and 19H05169), PRESTO (JPMJPR16NA), Support Program for Starting Up Innovation Hub from Japan Science and Technology Agency (JST), MEXT-KAKENHI (grant numbers 19H04692 and 16KK0097), FLAGSHIP2020 (project numbers hp190169 and hp190167 at K-computer), Toyota Motor Corporation, I-O DATA Foundation, Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049 and FA2386-19-1-4015), and JSPS Bilateral Joint Projects (with India DST).
April 1, 2021