Exploiting Symmetries: Speeding Up the computational study of Solid Solutions
Scientists develop software that can find all non-redundant substitution patterns in disordered systems, making computation in materials informatics faster
Substituting atoms in otherwise symmetric crystals is a widely used approach to tune the properties of materials for practical applications. In a recent study, JAIST scientists developed "SHRY," a software that can efficiently determine all unique substituted crystal structures for a given system by disregarding substitution patterns that are symmetric to others [https://github.com/giprayogo/SHRY]. Their method could speed up the estimation of the properties of novel and potentially useful solids.
Symmetry is a prevalent feature of nature at all scales. For example, our naked eyes can easily identify symmetries in the bodily shape of countless organisms. Symmetry is also very important in the fields of physics and chemistry, especially in the microscopic realm of atoms and molecules. Crystals, which are highly ordered materials, can even have multiple types of symmetry at the same time, such as rotational symmetry, inversion symmetry, and translational symmetry.
Lately, alongside rapid progress in computer science, researchers have developed computational methods that seek to predict the physical properties of crystals based on their electronic structure. In practice, however, pure and perfectly symmetric crystals are seldom used. This is because a crystal's properties can be tuned as desired by alloying them with other materials or randomly substituting certain atoms with other elements, i.e., doping.
Accordingly, materials scientists are seeking computationally efficient approaches to analyze such alloys and substituted crystals, also known as solid solutions. The 'supercell method' is one such approach and is widely used to model crystal structures with random substitutions of different atoms. The symmetry of crystals, however, is actually a problem when using this technique. In crystals, there can be many substitution patterns that are physically equivalent to other substitutions if we simply translate or rotate them. Findings these symmetric substitution patterns is not very meaningful, and thus their calculation when using the supercell method is a waste of time.
In a recent study, a team of researchers led by Assistant Professor Kousuke Nakano from Japan Advanced Institute of Science and Technology (JAIST) found a solution to this problem. They developed an open-source software called "Suite for High-throughput generation of models with atomic substitutions implemented by Python," or SHRY that can, in terms of symmetry, generate distinct substitution patterns in solid solutions and alloys [https://github.com/giprayogo/SHRY]. This work, which was published in the ACS Journal of Chemical Information and Modeling, was co-authored by doctoral student Genki I. Prayogo, Dr. Andrea Tirelli, Professor Ryo Maezono, and Associate Professor Kenta Hongo.
The team approached the problem from the angle of group theory. It turns out that searching for atomic substitution patterns in crystals is analogous to the problem of finding coloring patterns on the vertices of graphs under certain restrictions. This allows one to reformulate the original problem of finding non-symmetric atomic substitutions in crystals as exploring search trees depicting the coloring of vertices in graphs.
However, the way in which the search tree is explored is crucial. A simple, naïve approach in which all possible branches are searched and directly compared is impossible; the time and calculations required grow uncontrollably for large systems. This happens because deciding whether to explore further down a branch requires information about all other branches besides the one being explored, which is technically referred to as 'non-local information'.
To avoid this issue, the researchers implemented in SHRY a technique called canonical augmentation. "This method can decide whether a tree branch should be explored more deeply or not based solely on local information," explains Dr. Nakano, "Most importantly, theorems from group theory guarantee that only distinct substitution patterns will be extracted, without over- or under-exploring the tree structure in terms of symmetry." The team verified that their algorithm was error-free by testing it thoroughly with data from a database of crystal structures.
It is worth noting that SHRY was written in Python 3, one of the most popular cross-platform programming languages, and uploaded to GitHub, a leading project-sharing online platform. "SHRY can be used as a stand-alone program or imported into another Python program as a module," highlights Dr. Nakano, "Our software also uses the widely supported Crystallographic Information File (CIF) format for both the input and output of the sets of substituted crystal structures." The team plans to keep improving SHRY's code based on feedback from other users, boosting its speed and capabilities.
Overall, the software developed in this study could help scientists identify potential atomic substitutions in solids, which is the most common strategy used to tune the properties of materials for practical applications. SHRY will help speed up research and develop substituted crystals with unprecedented functionalities and superior characteristics.
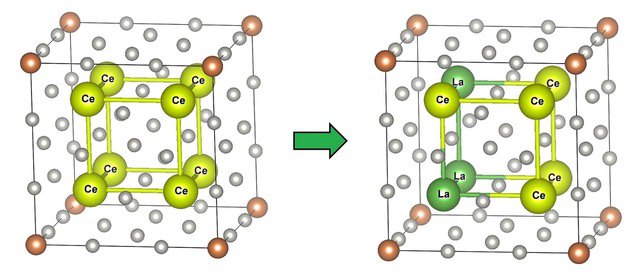
Figure 1. Example of an atomic substitution in a crystal
Atomic substitution with La atoms: Ce8Pd24Sb → (Ce5,La3)Pd24Sb. The crystal structure was obtained from the ICSD database (CollCode: 83378). The space group is 221-Pm3m, and the crystal structures are depicted using VESTA.
Image credit: Kousuke Nakano from JAIST.
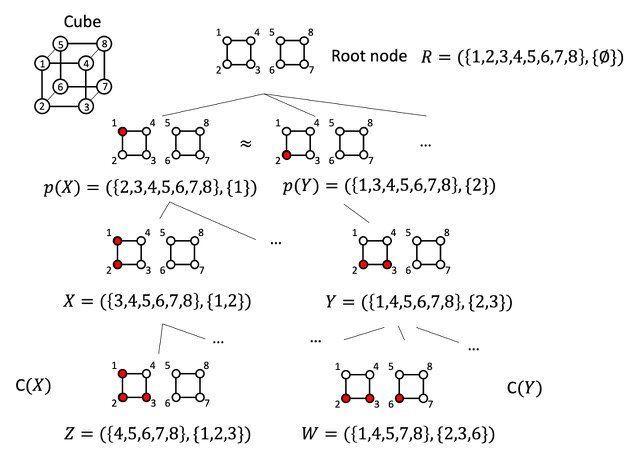
Figure 2. Example of a search tree representing an atomic substitution
In this search tree, three vertices out of eight are colored red in a cubic arrangement, representing the substitution of Figure 1. p(X) denotes the parent node of X, whereas C(X) denotes the set of children of X. Because of the symmetry of the cube, [p(X) and p(Y)], [X and Y] and [Z and W] are identical.
Image credit: Kousuke Nakano from JAIST.
Reference
| Title of original paper: | SHRY: Application of Canonical Augmentation to the Atomic Substitution Problem |
| Journal: | Journal of Chemical Information and Modeling |
| DOI: | 10.1021/acs.jcim.2c00389 |
Funding information
This work was financially supported by JST SPRING (Grant Number JPMJSP2102), MIUR Progetti di Ricerca di Rilevante Interesse Nazionale (PRIN) Bando 2017 (Grant Number 2017BZPKSZ), the HPCI System Research Project (Project IDs: hp210019,hp210131, and jh210045), MEXT-KAKENHI (JP16H06439, JP17K17762, JP19K05029, JP19H05169, JP21K03400, JP21H01998, JP22H02170, JP19H04692, and JP21K03400), the U.S. Air Force Office of Scientific Research (Award Number FA2386-20-1-4036, AFOSR-AOARD/FA2386-17-1-4049; FA2386-19-1-4015), JSPS Bilateral Joint Projects (JPJSBP120197714), JSPS Overseas Research Fellowships, a Grant-in-Aid for Early-Career Scientists (Grant Number JP21K17752), and a Grant-in-Aid for Scientific Research (C) (Grant Number JP21K03400).
June 28, 2022
