折り紙とパズルと多面体のページ
北陸先端科学技術大学院大学の
上原隆平が最近凝っている
- 折り紙,飛び出す絵本,ペーパークラフト(Origami, Pop-up book, Paper craft)
- パズル,不可能物体(Puzzle, Impossible object)
- 多面体,展開図(Polyhedron, Development or Net)
関連のページです.
イベント覚え書き・
ブログもどき・
上原の関連する結果へのリンク集・
その他のリンク集です.
出張その他で,うまくタイミングが会えば行きたいなぁと思っているイベント類や場所のメモです.
行けるかどうかは運次第 :-)
- 期間限定タイプ
- 期間はあまり関係ないところ
- 旭川ぱずるミュージアム:これは行ってみたいなぁ.
- 日本玩具博物館:玩具の収蔵品が9万点ほどあるとか.
本人の備忘録に近いメモ書きです.基本的には上に行くほど新しいです.
- 2025/10/18 パズル祭りと
トリトと
パズル懇話会
- ちょうど朝に海外出張から成田に帰国できたので,ちょうど同じ日に開催していた
パズル祭りというイベントと
パズル懇話会の例会に参加.移動途中で
トリトで買い物.以下覚書き:
 パズル祭り:
ペンシルパズル系のイベントでした.個人的には図形のパズルにハマってしまって,解けずに時間切れ...
パズル祭り:
ペンシルパズル系のイベントでした.個人的には図形のパズルにハマってしまって,解けずに時間切れ...
 パズル懇話会:
今日はやや参加者少なめで時間のゆとりがありました.100円ショップセリアで売っていたという箱入り娘と,
石井さんの「4方向から4つのシルエットが見える図形」を入手.
箱入り娘は,スタンダードな問題以外に,もっと手数のかかる問題が載っているのがすごいです.
誰が解析したのかな...
またシルエットの見える立体は,正4面体あるいは正8面体の軸を使うという発想が良いと思います.
パズル懇話会:
今日はやや参加者少なめで時間のゆとりがありました.100円ショップセリアで売っていたという箱入り娘と,
石井さんの「4方向から4つのシルエットが見える図形」を入手.
箱入り娘は,スタンダードな問題以外に,もっと手数のかかる問題が載っているのがすごいです.
誰が解析したのかな...
またシルエットの見える立体は,正4面体あるいは正8面体の軸を使うという発想が良いと思います.
 トリト:仕掛け屋定吉さんの新作を入手.
Facebookで見た印象よりもちょっと大きいです.自立するのがよいですね.
トリト:仕掛け屋定吉さんの新作を入手.
Facebookで見た印象よりもちょっと大きいです.自立するのがよいですね.
- 2025/10/10-11 高専プロコン in 松江

- 松江のくにびきメッセで開催された高専プロコンに審査員として参加しました.
そっちは省略して,せっかく松江に行くのでパズル仲間の内仲さんと晩御飯をご一緒しました.
その際に足立さんから預かってきたというパズルを3ついただきました.
「AntiSlide Sandwitches」と「SNOW FLAKES」と「収納上手6改」です.
相似なピースだけでこんなアンチスライドパズルが作れるとは,かなり驚きました.
すごいと思います.以前,アンチスライドパズルの困難性に関する論文を書きましたが,まだまだ奥深いものがあると感じさせます.
また松江の暮らしやすさも印象的でした.内仲さん,足立さん,ありがとうございました.
- 2025/09/26-29 IPP 42 in Tokyo


- 都内某所で開催されたIPP(International Puzzle Party)に参加.
今回も交換パズルを自作して参加したので,70個以上の新作パズルを入手しました.
それとは別に,既存のパズルや本もいくつか購入.数が多すぎて書ききれないので,書きませんが,
いろいろと論文になりそうなタネやネタも手に入り,大満足です.
また,スタッフの記念品や,ゲーム大会の景品も手に入り,ラッキーでした.
関係者の皆様,お疲れ様でした.
- 2025/09/12-14 広州出張

- 中国の広州でCJCGGG 2025という会議に参加・発表.
自分の関係する発表は2件.
- Ryuhei Uehara.
Undecidable Puzzles (Plenary Talk),
The 27th China-Japan Conference on Discrete and Computational Geometry, Graphs, and Games,
2025/09/12-14, Guangzhou, China.
- Yanqiu Tan, Tonan Kamata and Ryuhei Uehara.
Computational Complexity on Hexa Gravity Puzzles,
The 27th China-Japan Conference on Discrete and Computational Geometry, Graphs, and Games,
2025/09/12-14, Guangzhou, China.
基調講演の方は,最近気になっている「原理的にコンピュータで解けない問題」についてまとめて話すことができて,満足しました.
Erik DemaineやStefan Langermanの基調講演と興味が共通する部分が多くて,そちらも得るものが多かったです.
また知り合いのSupanut Chaideeが発表したMagnetic Battle Chessというゲームがすごく面白いなぁと思っていたところ,
みんなでお土産を物色しに行った近所のスーパーで売っているのを偶然発見.日本人集団+Stefanで買い占めました.
- 2025/09/07 誕生日

- トリトで買ったパズルが届いて,自分用の誕生日プレゼントになりました.
文字キューブはフォントの研究になりそうな気がします.
Cast Walletはスライドして詰めるパズルの2次元バージョンの典型例かと思います.
CoggyとCrankityは現時点ではいろいろと考え中.
- 2025/09/06 誕生日前日


- 上原研究室の卒業生が中心となって,還暦誕生日パーティーを開いてくれました.30名以上も参加してくれて,感激しました.
オーダーメードの特注ケーキにはPeg Solitaire Fontで文字が書いてありました.すごいものを作ってもらったんだなぁ...
また,私の誕生日ということで,パズルっぽいものをいろいろといただきました.備忘のためにメモしておきます.
- ペントミノチョコレート: なんとこちらもオーダーメードの特注品です.ありがたや...
- Ghost Hunters: こちらは学生からいただきました.Smart Games社の製品は,かなり持っているのですが,幸い重複はしませんでした.
- タイリングの皿: 金箔でタイリングが描いてあります.実物を作れば,1自由度で動く模様になっています.
- Invertible Void: 天童さん自作のカレイドサイクル.紅白でめでたい感じです.
- Parent-child Trapezoids: 三浦さんのパズル.なかなか手ごわい...
パズルっぽくないもの,おいしいものもたくさんいただきました.
関係者の皆様,ありがとうございます.120歳目指してがんばります.
- 2025/08/11-15 カナダ出張

- カナダのトロントでCCCG/WADS 2025という会議に参加.
これは二つの会議WADSとCCCGの同時開催で,私は日程の関係上CCCGの方だけ参加.自分の名前が入っているのは以下の3本.
- Takeshi Yamada, Tom van der Zanden, and Ryuhei Uehara.
Puzzles are hard enough just by rotations,
The 37th Canadian Conference on Computational Geometry (CCCG 2025),
pp. 211-215, 2025/08/13-2025/08/15, Toronto, Ontario, Canada.
- Takumi Shiota, Yudai Enomoto, Masashi Gorobe, Takashi Horiyama, Tonan Kamata, Toshiki Saitoh, and Ryuhei Uehara.
The Number of Non-overlapping Unfoldings in Convex Polyhedra,
The 37th Canadian Conference on Computational Geometry (CCCG 2025),
pp. 133-139, 2025/08/13-2025/08/15, Toronto, Ontario, Canada.
- MIT CompGeom Group, Hugo A. Akitaya, Erik D. Demaine, Adam Hesterberg, Thomas C. Hull, Anna Lubiw, Jayson Lynch, Klara Mundilova,
Chie Nara, Joseph O'Rourke, Frederick Stock, Josef Tkadlec, and Ryuhei Uehara.
Quasigeodesics on the Cube,
The 37th Canadian Conference on Computational Geometry (CCCG 2025),
pp. 78-84, 2025/08/13-2025/08/15, Toronto, Ontario, Canada.
タイから台北を経由してアメリカに移動する途中,台北でほぼ全員の荷物がロストするという驚きのトラブルに巻き込まれ,
その後,荷物はNYのJFKに到達するものの手元にはたどり着かず,そのままカナダに移動しました.
さすがにいろいろと足りなくなり,ホテルの隣にあったWalmartでいろいろと買い物.その途中でULTIMATE Tic-Tac-Toeというゲームを見つけてつい購入.
小さい盤面で決着がつくと,大きい盤面の1マスが決まるというメタなTic-Tac-Toeです.
計算量的な興味からは,再帰的に繰り返すと面白いかな?と思っています.人間がやるとついていけなさそうですが.
- 2025/08/10-12 アメリカ出張


- アメリカのNYでMOVES 2025という会議に参加.
自分の名前の入っている発表は以下のもので,発表は半分づつ.
- Erik D. Demaine, Martin L. Demaine, Tonan Kamata, Tomoko Taniguchi, and Ryuhei Uehara.
Tilt Fonts, MOVES 2025, 2025/08/10-12, NY, USA.
MOVESはMoMathことMuseum of Mathematicsが主催する各年開催の会議です.
会議参加者へのお土産パズルが盛り沢山です.自分で買ったパズルもいくつか.
特にEgyptian Triglyphというパズル,正4面体の枠組にSOMA CUBEを埋め込むパズルで,なかなか興味深いです.
- 2025/08/06-08 タイ出張

- タイのチェンマイでAFGS 2025という会議に参加.
自分の名前の入っている発表は以下のものですが,発表は谷口さんにお任せ.
会議の最終日の空き時間に,知り合いの先生に学内のあちこちを案内してもらいました.ありがとうございました.
エクスカージョンで行った先で,4面体のポーチと,箱入り娘を見つけて購入.箱入り娘は古典的なパターンですが,
「ボールを下に落とせ」というわかりやすい出題形式がなかなか良いと思います.
- 2025/08/03 東京弾丸出張


- またまた東京に弾丸出張.移動のスキマ時間を利用して,銀座の三越でやっているカラクリの展示と,
白山のおりがみはうすに行ってきました.Google Mapで経路検索すると,都内の移動時間の短さを感じます.
かつて東京に30年も住んでいたのに,予想外の経路が出てきて興味深いです.
- 2025/07/31 東京弾丸出張


- 東京に弾丸出張して,ホリエモンこと堀江貴文氏と対談してきました.
対談の中身は8月下旬か9月上旬にNewsPicksの中の
HORIE ONEというところに出る予定です.
パズルと折り紙とアルゴリズムの話をいろいろとしてきました.
帰りにKITTEの地下を通ったら,防災グッズのフェアをやっていて,そこで
折り紙食器beakの展示を見つけて,営業の人と少しお話ししました.
こういう観点の展開図,応用範囲は広そうです.
- 2025/07/11 沖縄草玩具館
-
とある沖縄の企業と共同研究を開始したのですが,そのスキマ時間に
沖縄草玩具館につれていっていただきました.
感激しました.特に館長の新崎宏氏の熱いトークには胸を打たれました.沖縄は暑くて熱い!

- まず事前に電話連絡が必要です.場所は住宅街の行き止まりなので,よく調べて行く必要があります.

- 入場料はかかりませんが,時間は(かなり)かかります.いろんなお話を伺って,いろいろと作って,
楽しくて密度の濃い時間が過ごせます.

- 入場券も何故か6枚セットで,いろんな草紐の編み方が書いてあります.
 かなり昔,沖縄のジュンク堂で「手遊び草編み玩具」の1〜3巻を偶然見つけて入手して以来,
ずっと行きたかったところに行けて,大変感激しました.10日にジュンク堂で調べてもらって,
第4巻は無事に入手できたのですが,別巻の「草ひも」はジュンク堂でも入荷したことがないそうで,
玩具館で直接館長から譲っていただきました.どれも熱い思いが詰まった本で,面白いです.
かなり昔,沖縄のジュンク堂で「手遊び草編み玩具」の1〜3巻を偶然見つけて入手して以来,
ずっと行きたかったところに行けて,大変感激しました.10日にジュンク堂で調べてもらって,
第4巻は無事に入手できたのですが,別巻の「草ひも」はジュンク堂でも入荷したことがないそうで,
玩具館で直接館長から譲っていただきました.どれも熱い思いが詰まった本で,面白いです.
- 2025/06/末 いろんな計算器が届く

-
とある方から,いろいろな計算器を送っていただきました.ありがとうございます.
タイガーの手回し式計算器には「東京女子大学」のシールが貼ってありました.
これが辿ってきた経路を考えると感慨深いです.
そういえば昔の私は,東京女子大学の歴史始まって以来の初めての男性の助手だったそうです.懐かしいです.
- 2025/06/28-29 第38回折り紙の科学・数学・教育研究集会

-
折り紙の会議に出るために北海道大学へ.私の名前の入った発表は以下の4件.
- Erik D. Demaine, 上原 隆平, 鎌田 斗南.
Dudeney's Dissection is Optimal,
第38回折り紙の科学・数学・教育研究集会,
2025/06/28-29.
- 舩倉 大和, 上原 隆平, 鎌田 斗南, 谷口智子.
牛乳パックを使った立体容器の産学共同研究,
第38回折り紙の科学・数学・教育研究集会,
2025/06/28-29.
- 塩田 拓海, 鎌田 斗南, Jason S. Ku, 上原 隆平.
Edge Overlap-Freeness in Regular Prisms with a Continuous Parameter,
第38回折り紙の科学・数学・教育研究集会,
2025/06/28-29.
- 谷口 智子, 上原 隆平.
アインシュタイン・タイリング・フォント,
第38回折り紙の科学・数学・教育研究集会,
2025/06/28-29.
石塚王子と共同開発したパックポンのORIGAMIバージョンも配布しました.
- 2025/06/28 羽田空港の年輪屋の箱


- 金沢から羽田経由で北海道に移動中,羽田空港の年輪屋で変わったバウムクーヘンの箱を見つけて,
箱買いしました.中身はスタッフとおいしくいただきました.正四面体の箱はたまに見かけますが,
開ける口のデザインが秀逸です.中身を出したあと,平坦に折り畳めるところもすばらしい.
- 2025/06/23-27 CGWeek 2025/SoCG 2025 in Kanazawa


- 金沢でCGWeekという国際会議を運営していました.これは計算幾何学のトップカンファレンスで,200名以上の参加者があり,盛況でした.
会議の記念品をガチャポンで配り,そこに最近,石塚王子と共同開発したパックポンを
使ってみました.
合間を縫ってErikをJAISTで雇用するための手続きをしたり,
大学のプレスリリース用に写真撮影をしたりなど,
バタついていましたが,Erikや舘さんや野老さんなど,豪華なメンバーが参加して,楽しかったです.
会場のWasha-WashaエリアにErikが出していたパズルの中に,以下の論文の図の実物がありました.
現物が作られたのは,初めてだと思います.
- 2025/06/01 香港で買い物
- とある国際会議があって香港に出張.最終日にちょっと時間ができたので,女人街とCat Streetに行ってきました.

- Cat Street:上環駅から山に向かって登っていくとある,骨董品屋街です.
ものすごい高級品から,ものすごいB級品まであって,楽しいです.昔はもっといかがわしいものがたくさんあったのですが,
だいぶ大人しくなりました.ある店で,「人間がたくさん集まって人間になっている」像があったので,見せてもらいました.
わりと下ネタ系で,上の蓋が開くと,中からエロいものが出てきます.作りはとても良いのですが,
ネタで買うには,お値段がヤバすぎたので,見せてもらうだけ.

- 女人街:旺角駅のそばにある出店のストリートです.女人が売ってるわけではなく,女性服などがたくさん売っています.
ブランドのパチモノも売るほど溢れています.丁寧に端の方まで歩いていくと,キューブ系のパズルなどをたくさん売っている
店もチラホラあって,楽しめます.
 結局,女人街では3x3x1のキューブがフィジェットになって,高速回転するものを買いました.
よく調べてみると,市販の3x3x1のキューブよりも自由度が高くて,簡単に戻せることがわかりました.
市販の3x3x1のキューブは稼働できる配置が異なる2バージョンあるので,これもいれると,3バージョンあることになり,興味深いです.
買って正解でした.
Cat Streetでは,アクセサリを売っている店で,金属の多面体を見つけて購入しました.とはいっても,棒がついていて,棒には穴が空いてます.
用途はわかりません.重くて,マドラーでもなさそうだし,風鈴の中にぶら下げるのかなぁ...?
結局,女人街では3x3x1のキューブがフィジェットになって,高速回転するものを買いました.
よく調べてみると,市販の3x3x1のキューブよりも自由度が高くて,簡単に戻せることがわかりました.
市販の3x3x1のキューブは稼働できる配置が異なる2バージョンあるので,これもいれると,3バージョンあることになり,興味深いです.
買って正解でした.
Cat Streetでは,アクセサリを売っている店で,金属の多面体を見つけて購入しました.とはいっても,棒がついていて,棒には穴が空いてます.
用途はわかりません.重くて,マドラーでもなさそうだし,風鈴の中にぶら下げるのかなぁ...?
- 2025/05/11 東京で買い物


- 所要があって東京にお出かけ.パズルイベントにも参加しました.以前から欲しかったものなどが入手できて,大満足しました.
自作パズルの新作Zweisteinを配って皆さんに解いていただきました.楽しんでもらえたようで何よりです.
先月買った3Dのシルエットパズルの他のものも一通り購入しました.いろいろと論文のネタになりそうな予感がします.
- 2025/04/25-26 関東弾丸出張


- 所要があって関東に弾丸出張.駅前で時間つぶしにセリアに入ってみたところ,
楽しそうなものがいろいろと.Smart Puzzleは古典的なアレですが,これが100円で買えるとは.
Impossible pyramidは以前から気になっていて,どこかでいつか買いたいなぁと思っていた玩具です.
これまた100円で買えるとは,驚きです.
帰りの新幹線の時間調整で,トリトさんにもパトロールに行きました.
Acazuさんのsnail,枠が二つあって「どちらかの枠には収まりません」という大胆な出題.これはキツい.
他方のシルエットLOGは3方向からの影の形が出題されるというもの.ちょっと古いものですが,出題が秀逸だと思います.
これは知りませんでした.
- 2025/04/21 Puzzle Matches

- 京都の寺町を移動中,ものすごく良い感じの古物商を見つけたので探索.
4センチ立方の1x1x1のルービックキューブっぽいものを見つけて救済.
開けてみると,puzzle matchesと書いてあるマッチ箱のセットでした.
中にはマッチが4箱入っていて,表と裏が絵合わせになっています.
裏の図柄は迷路になっていて4つでもつながります.
表の図柄は完成しなくて,どうも,本来は12個くらいのセットである気がします.
- 2025/02/14-24 MIT訪問
- 久しぶりにアメリカのボストンにあるMITで研究の打合せ.研究内容はスキップして,パズルっぽい備忘録を.
- Eureka!:
 ボストンで外せないパズルショップ.以前はもう一件Harvardの近くにもあったのですが,残念ながら閉店してしまいました.
Eureka!ではIPPの交換品パズルなどもちょっと売っていて,なかなかマニアックな品物もありますが,一般向けのパズルや玩具も多くて楽しめます.
今回は本を1冊と,最近気になっている「円形ベース」のパズルを2点.
ボストンで外せないパズルショップ.以前はもう一件Harvardの近くにもあったのですが,残念ながら閉店してしまいました.
Eureka!ではIPPの交換品パズルなどもちょっと売っていて,なかなかマニアックな品物もありますが,一般向けのパズルや玩具も多くて楽しめます.
今回は本を1冊と,最近気になっている「円形ベース」のパズルを2点.
- Quincy Market:
 Quincy Marketにはいろいろと楽しい店があり,
ボストンに来ると外せないところですが,その中にMuseum of Illusionsという楽しげな
博物館を見つけました.入場料は高いですが,Museum Shopにはタダで入れます
入ってみると,古典的なパズルがけっこう売っていて楽しめました.15パズルの拡張版の24パズルと,Devil Cube Puzzleを購入.
あとはキーホルダー.スマホ型のお菓子は空港で見つけて買ったものが写り込んでいます.
Quincy Marketにはいろいろと楽しい店があり,
ボストンに来ると外せないところですが,その中にMuseum of Illusionsという楽しげな
博物館を見つけました.入場料は高いですが,Museum Shopにはタダで入れます
入ってみると,古典的なパズルがけっこう売っていて楽しめました.15パズルの拡張版の24パズルと,Devil Cube Puzzleを購入.
あとはキーホルダー.スマホ型のお菓子は空港で見つけて買ったものが写り込んでいます.
- (In)Secure Cree Bruins in collaboration with Martin and Erik Demaine:
 MITのErik DemaineとMartin DemaineがQRコードとか折り紙に関する作品をいくつかデザインして展示しているとのことで,
本人の案内で見学に行きました.いろいろと刺激的で楽しい展示でした.
MITのErik DemaineとMartin DemaineがQRコードとか折り紙に関する作品をいくつかデザインして展示しているとのことで,
本人の案内で見学に行きました.いろいろと刺激的で楽しい展示でした.
- MIT Museum:
 Kendall駅の前に移転しておしゃれになったMIT博物館.いつもMuseum Shopしか行きませんが...
今回はActivating Origamiを購入.
折り紙と折り図と回路が入っていて,振動させたり光らせたりできます.
折り紙を振動させたり光らせたりしてどうすんだとか言ってはいけません.
さすがMITっぽいものを売ってるなぁと思う次第.
Kendall駅の前に移転しておしゃれになったMIT博物館.いつもMuseum Shopしか行きませんが...
今回はActivating Origamiを購入.
折り紙と折り図と回路が入っていて,振動させたり光らせたりできます.
折り紙を振動させたり光らせたりしてどうすんだとか言ってはいけません.
さすがMITっぽいものを売ってるなぁと思う次第.
- Boston Antique Market:
 BostonのグリーンラインのLechmere駅から歩いてすぐのところにあるアンティークショップ.地上4階地下1階に,
ぎっちりアンティークショップが入っていて,かなり楽しいです.以前は入場料がかかった覚えがあるけれど,
無料になっていました.駅近辺もすごく綺麗になっていて雰囲気が明るくなりました.
今回は以下の5つを購入.散財しました.
BostonのグリーンラインのLechmere駅から歩いてすぐのところにあるアンティークショップ.地上4階地下1階に,
ぎっちりアンティークショップが入っていて,かなり楽しいです.以前は入場料がかかった覚えがあるけれど,
無料になっていました.駅近辺もすごく綺麗になっていて雰囲気が明るくなりました.
今回は以下の5つを購入.散財しました.
- Shmuzzles: Tesselation Toysと書いてあるとおり,タイリングのおもちゃです.
重さがけっこうあったので,材料が気になりましたが,厚紙製でした.
- Kaji or Jan-Ken-Po: トランプっぽいけれど,ジャンケンもできるカードゲームです.
カードでジャンケンしなくてもいいんじゃ?とか言ってはいけません.
- 石製の多面体: 立方八面体の石のオブジェを見つけました.ちょっと変わった石で,
しかもちょっとデカいです.もちろん持ち帰るのは重かったです.
- ウサギのオブジェ: 一見すると気づきにくいのですが,どうもタングラムを意匠化したものと思われます.
細かく見るとバランスがおかしいので,そこが逆に面白いと思います.金属製でそこも良いです.
- Multipurpose Ruler: いろんな長さが測れるモノサシなのですが,金属ローラーまでついていて,
「そんなのはいらなくないか?」と思わせるところがグッときます.
あとで考えると,重いものばかり買ってます.デカいスーツケースを持ってきて正解でした.
- 2025/01/27-29 2024年度冬のLAシンポジウム

- 日本で最も歴史のある理論計算機の会議の一つ,LAシンポジウムに行ってきました.
50年以上の歴史があり,冬は京都大学の数理解析研究所でやることが多いです.今回は私の関係する発表はたくさんありました:
- 後藤 大河, 鎌田 斗南, 上原 隆平.
不動点伝播法による共通展開図の構成,
冬のLAシンポジウム, pp. 28S:1-7, 2025/01/27.
- 能美 雄太, 塩田 拓海, 鎌田 斗南, 上原 隆平.
Dissections of a Net of a Regular Octahedron into Nets of Regular Octahedra,
冬のLAシンポジウム, pp. 27S:1-9, 2025/01/27.
- 鎌田 斗南, Jason S. Ku, 塩田 拓海,上原 隆平
Edge Overlap-freeness of Prisms with a Continuous Parameter,
冬のLAシンポジウム, pp. 26S:1-16, 2025/01/27.
- Erik D. Demaine, Tonan Kamata, Ryuhei Uehara.
Dudeney’s Dissection is Optimal
冬のLAシンポジウム, pp. 25:1-19, 2025/01/27.
- QIAN, Mengze, Ryuhei Uehara.
Efficient Enumeration of Block-Cutpoint Trees,
冬のLAシンポジウム, pp. 1:1-7, 2025/01/27.
グラフアルゴリズム,パズル,計算折り紙とてんこ盛りです.LAは日本の会議で,共同で開催しているEATCS日本支部というのがあります.
これはヨーロッパの理論計算機科学の学会です.これらが共同して出しているLA/EATCS-Japan presentation awardという
プレゼンテーションの賞があるのですが,上記の「デュードニーの分割の最小性の証明」を発表した鎌田くんがみごとに受賞しました.
おめでたいです.
帰りに京都大学の博物館に寄って,京大工房の2進数トランプっていうのを見つけて買ってみました.
情報系の学生にささるかな.
- 2025/01/22 微妙な任務で東京出張


- 微妙な任務で東京に日帰り出張.移動の時間調整で,
OAZOと「おりがみはうす」と「奥野かるた」でもろもろ買い物.
OAZOではかなり珍しい形の箱のチョコレートを見かけて購入.
ちょっと広がった6角柱に丸い屋根がついた形をしています.展開図が絶妙です.
地下のCAN DO!で「パステル3Dパズル」というプラスチック製の組み木を購入.4種類あるみたいだけど,2つしか売ってなかった...
一方は古典的なパターンだけど,他方はちょっと微妙なので気になります.
奥野かるたでは,12面体サイコロとベーゴマを購入.12面体サイコロはいくつか持っているけど,数字じゃなくて点々が
書いてあるのは初めてみました.点々が多いと,パッと見てもわからないかもしれません.
ベーゴマ,たぶん50年ぶりくらいに手にしました.まだ回せるかなぁ...
おりがみはうすでは,勝田さんの本を2冊と,キーホルダーを購入.御本人から買いました.
- 2025/01/10 難しいパズル届く
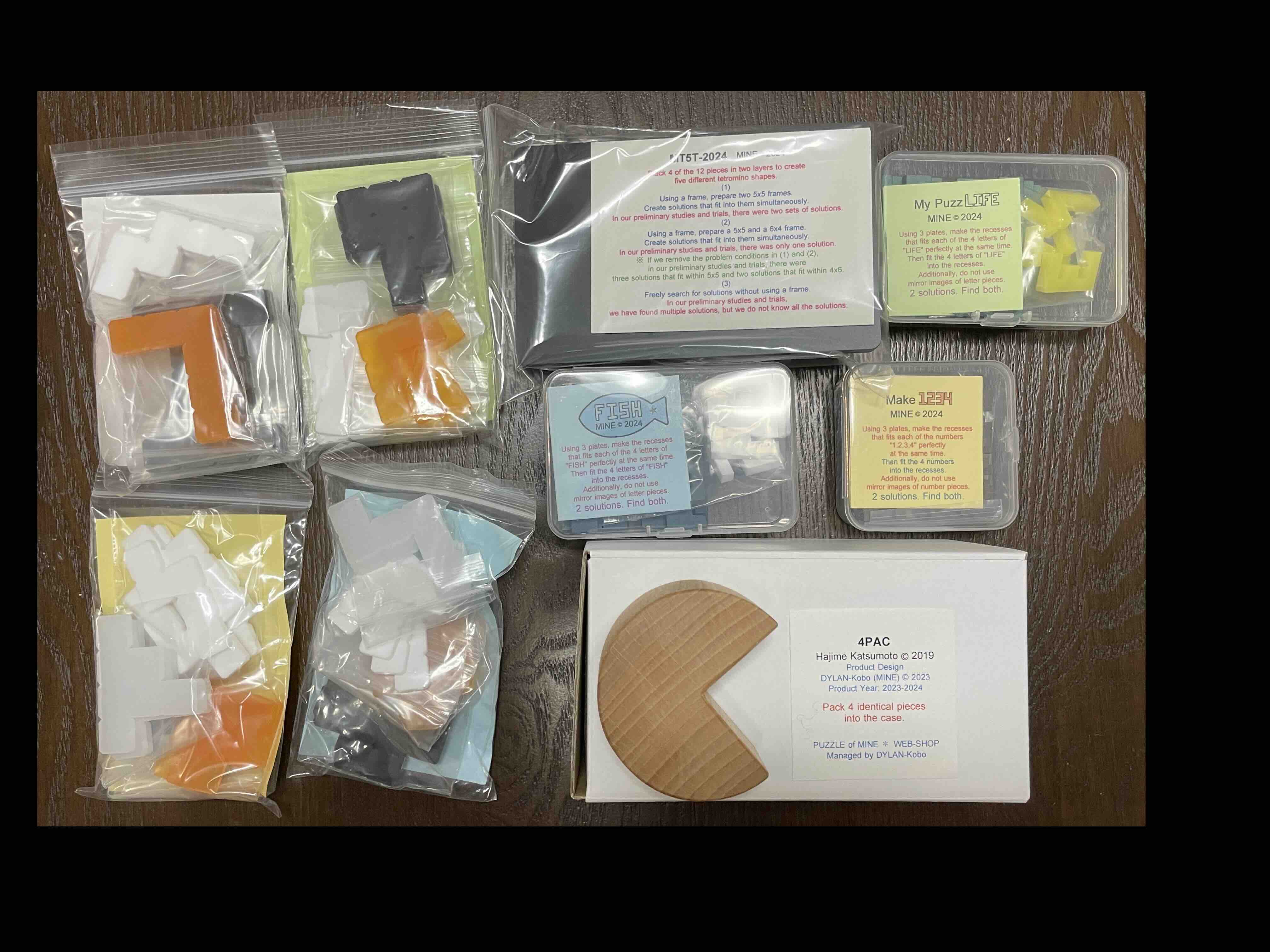
- MINEさんに注文しておいたパズルが届きました.
どれも難しくて楽しめそうです.特に気になっていたのが4PACなのですが,さすがに簡単には解けません...
備忘のためにパズル名を書いておきます:4PAC, MT5T-2024, Make1234, My PuzzLIFE, FISH, MVM, MWM, MXM, MYM.
- 2025/01/06 パズル届く

-
カナダの郵便のストライキで遅れていたパズルが届いていました.なかなか良さそうな論文のタネの匂いがします.
最初の2つの外れ方は写真から想像がついていたのですが,3つ目がちょっと予想外でした.
- 古いエントリー
-
2024年|
2023年|
2022年|
2021年|
2020年|
2019年|
2018年|
2017年|
2016年|
2015年|
2014年|
2013年|
2012年|
2011年|
2010年|
2009年|
2008年以前
以下,上原が折り紙,パズル,多面体に関しておこなった研究のごく簡単な解説とリンクです.
アカデミックな業績とその他と分けてあります.
ただしアカデミックかどうかは主観によるかもしれません.
-



 書籍:『完全版マーティン・ガードナー数学ゲーム全集』
書籍:『完全版マーティン・ガードナー数学ゲーム全集』
- マーティン・ガードナーの数学ゲーム全集の翻訳です.
プロジェクトとしては全15巻シリーズになる予定で,原著は4巻まで出ています.
日本語版は1,2巻は2015年,3巻は2016年,4巻は2017年に出ました.
-

 書籍編集『ORIGAMI6』
書籍編集『ORIGAMI6』
- 折り紙のサイエンスに関する国際会議
6OSME(The 6th International Meeting on Origami in Science,
Mathematics and Education)の会議録(論文集)です.私の書いた論文も載ってます.
アメリカ数学会(AMS)から出ています.
 書籍:『はじめてのアルゴリズム』
書籍:『はじめてのアルゴリズム』
- 書き下ろしです.近代科学社の『はじめての〜』シリーズの一つです.
サポートページもあります.
アルゴリズムを理解するためのパズルとして,ハノイの塔,エイト・クイーン,ナイトの巡回問題などを取り上げました.
あとは細かい小ネタにパズルっぽい話がちらほらとあります.
 書籍:『折り紙のすうり』
書籍:『折り紙のすうり』
- 原著は``How to Fold It:
The Mathematics of Linkages, Origami, and Polyhedra''という本で,
著者はJoseph O'Rourkeです.
原著のサポートページと
邦訳のサポートページがあります.
 書籍:『ゲームとパズルの計算量』
書籍:『ゲームとパズルの計算量』
- 原著は"Games, Puzzles, & Computation"という本で,
著者はRobert A. Hearnと
Erik D. Demaineです.
原著のサポートページと
邦訳のサポートページがあります.
 書籍:『幾何的な折りアルゴリズム』
書籍:『幾何的な折りアルゴリズム』
- 原著は``Geometric Folding Algorithms: Linkages, Origami, Polyhedra''という本で,
著者はErik D. Demaineと
Joseph O'Rourkeです.
原著のサポートページと
邦訳のサポートページがあります.
- じゃばら折りの複雑さに関する研究
- じゃばら折りや,その一般化パターンを効率よく折ることについての研究をしています.
-
じゃばら折りや,その一般化パターンに対して,高速に折り目をつける方法を研究しました.
紙を重ねて折れば相当効率よく折り目をつけることができます.このテーマについては,
以下の国際会議での発表が一番詳しいです.
-
じゃばら折りの折りたたみ方は1通りしかないですが,一般の山谷パターンの折りたたみ方は
たくさんあります.指数関数的に多いです.そうした多くの選択肢の中から,
紙の延びを最小化する折りたたみを見つけるための研究をしています.このテーマについては,
今のところ以下の国際会議での発表が一番詳しいです.
いずれ以下の国際会議の会議録が出たら,それが一番詳しいものになるはずです.
- 複数の箱を作ることができる展開図
- 以下の各種のページを御覧下さい.
- 飛び出す絵本のNP完全性
- 以下の本に掲載されてるのが一番詳しいです.
- 浮き出し迷路の生成アルゴリズム
- 浮き出し迷路(答を塗りつぶすと絵になる迷路)を自動的に生成するアルゴリズムに関する研究です.
東工大の岡本さんと私とで最初に発表した論文が
で,論文そのものはここにあります.
そのあと,いくつかの拡張が行われました.
岡本さんがここにまとめてくれています.
- 折り紙の決定不能問題
- 折り紙を「実数平面」と考えると,ちょっとおかしな定理が示せます.
ほとんどの実数は「折れない」ため,折り紙の上のほとんどの点は「正確に折る」ことができません.
その議論をさらに進めると,与えられた点を折れるかどうか,有限の時間内で判定できなくなります.
こうした結果を以下で発表しました.
この結果をどう受け止めたらいいのか,私もよくわかりません.
- ↓以下,そのうち書きます.↓
- Voronoiゲームの複雑さ
- 一般化Hi-QのNP完全性
- 一般化KaboozleやシルエットパズルのNP完全性
- 一般化UNOの複雑さ
- 『折紙探偵団コンベンション折り図集Vol.15』

- 私がデザインした「目玉」が掲載されています.
- 『北陸おりがみコンベンション折図集Vol.5』

- 私がデザインした「市松サイコロ」が掲載されています.
講習会で取り上げた「十字架」や「組めるパターン/組めないパターン」もおりを見てまとめてどこかに出したいです.
- 『北陸おりがみコンベンション折図集Vol.6』

- 石川在住のパズル作家,山本浩さんと
コラボした作品「不思議な立体」が載っています.
1枚の紙に切れ目を入れて折るだけで,かなり面白い立体もどきが作れます.
- 幾何的な玩具類
- 展開図などの研究をするときに便利な玩具類を集めたページです.
- 個人のブログなど
- 前川さん|
三谷さんの
ブログ|
古田さん|
舘さん|
羽鳥さん|
北條さん|
R. Langさん|
R. Sabudaさん|
GFALOP|
創造する玩具|
幾何学おもちゃの世界|
ペーパークラフトと科学教育|
Printable Paper|
- 会社や団体など
- 折り紙探偵団|
Origami BBS|
ポップアップカードデザイナー|
グラフテック社の
Craft ROBO|
AssistOn|
かみの工作所|
美創印刷株式会社|
ジャバラミュージアム|
竹尾|
東京紙器
- 折り紙の科学・数学・教育研究集会
-
第1回|
第2回|
第3回|
第4回|
第5回|
第6回|
第7回|
Last modified: Sun May 31 21:19:58 JST 2015
by Ryuhei Uehara (uehara@jaist.ac.jp)
| 
|
 パズル祭り:
ペンシルパズル系のイベントでした.個人的には図形のパズルにハマってしまって,解けずに時間切れ...
パズル祭り:
ペンシルパズル系のイベントでした.個人的には図形のパズルにハマってしまって,解けずに時間切れ...
 パズル懇話会:
今日はやや参加者少なめで時間のゆとりがありました.100円ショップセリアで売っていたという箱入り娘と,
石井さんの「4方向から4つのシルエットが見える図形」を入手.
箱入り娘は,スタンダードな問題以外に,もっと手数のかかる問題が載っているのがすごいです.
誰が解析したのかな...
またシルエットの見える立体は,正4面体あるいは正8面体の軸を使うという発想が良いと思います.
パズル懇話会:
今日はやや参加者少なめで時間のゆとりがありました.100円ショップセリアで売っていたという箱入り娘と,
石井さんの「4方向から4つのシルエットが見える図形」を入手.
箱入り娘は,スタンダードな問題以外に,もっと手数のかかる問題が載っているのがすごいです.
誰が解析したのかな...
またシルエットの見える立体は,正4面体あるいは正8面体の軸を使うという発想が良いと思います.
 トリト:仕掛け屋定吉さんの新作を入手.
Facebookで見た印象よりもちょっと大きいです.自立するのがよいですね.
トリト:仕掛け屋定吉さんの新作を入手.
Facebookで見た印象よりもちょっと大きいです.自立するのがよいですね.


















 かなり昔,沖縄のジュンク堂で「手遊び草編み玩具」の1〜3巻を偶然見つけて入手して以来,
ずっと行きたかったところに行けて,大変感激しました.10日にジュンク堂で調べてもらって,
第4巻は無事に入手できたのですが,別巻の「草ひも」はジュンク堂でも入荷したことがないそうで,
玩具館で直接館長から譲っていただきました.どれも熱い思いが詰まった本で,面白いです.
かなり昔,沖縄のジュンク堂で「手遊び草編み玩具」の1〜3巻を偶然見つけて入手して以来,
ずっと行きたかったところに行けて,大変感激しました.10日にジュンク堂で調べてもらって,
第4巻は無事に入手できたのですが,別巻の「草ひも」はジュンク堂でも入荷したことがないそうで,
玩具館で直接館長から譲っていただきました.どれも熱い思いが詰まった本で,面白いです.








 結局,女人街では3x3x1のキューブがフィジェットになって,高速回転するものを買いました.
よく調べてみると,市販の3x3x1のキューブよりも自由度が高くて,簡単に戻せることがわかりました.
市販の3x3x1のキューブは稼働できる配置が異なる2バージョンあるので,これもいれると,3バージョンあることになり,興味深いです.
買って正解でした.
Cat Streetでは,アクセサリを売っている店で,金属の多面体を見つけて購入しました.とはいっても,棒がついていて,棒には穴が空いてます.
用途はわかりません.重くて,マドラーでもなさそうだし,風鈴の中にぶら下げるのかなぁ...?
結局,女人街では3x3x1のキューブがフィジェットになって,高速回転するものを買いました.
よく調べてみると,市販の3x3x1のキューブよりも自由度が高くて,簡単に戻せることがわかりました.
市販の3x3x1のキューブは稼働できる配置が異なる2バージョンあるので,これもいれると,3バージョンあることになり,興味深いです.
買って正解でした.
Cat Streetでは,アクセサリを売っている店で,金属の多面体を見つけて購入しました.とはいっても,棒がついていて,棒には穴が空いてます.
用途はわかりません.重くて,マドラーでもなさそうだし,風鈴の中にぶら下げるのかなぁ...?





 ボストンで外せないパズルショップ.以前はもう一件Harvardの近くにもあったのですが,残念ながら閉店してしまいました.
Eureka!ではIPPの交換品パズルなどもちょっと売っていて,なかなかマニアックな品物もありますが,一般向けのパズルや玩具も多くて楽しめます.
今回は本を1冊と,最近気になっている「円形ベース」のパズルを2点.
ボストンで外せないパズルショップ.以前はもう一件Harvardの近くにもあったのですが,残念ながら閉店してしまいました.
Eureka!ではIPPの交換品パズルなどもちょっと売っていて,なかなかマニアックな品物もありますが,一般向けのパズルや玩具も多くて楽しめます.
今回は本を1冊と,最近気になっている「円形ベース」のパズルを2点.
 Quincy Marketにはいろいろと楽しい店があり,
ボストンに来ると外せないところですが,その中にMuseum of Illusionsという楽しげな
博物館を見つけました.入場料は高いですが,Museum Shopにはタダで入れます
入ってみると,古典的なパズルがけっこう売っていて楽しめました.15パズルの拡張版の24パズルと,Devil Cube Puzzleを購入.
あとはキーホルダー.スマホ型のお菓子は空港で見つけて買ったものが写り込んでいます.
Quincy Marketにはいろいろと楽しい店があり,
ボストンに来ると外せないところですが,その中にMuseum of Illusionsという楽しげな
博物館を見つけました.入場料は高いですが,Museum Shopにはタダで入れます
入ってみると,古典的なパズルがけっこう売っていて楽しめました.15パズルの拡張版の24パズルと,Devil Cube Puzzleを購入.
あとはキーホルダー.スマホ型のお菓子は空港で見つけて買ったものが写り込んでいます.
 MITのErik DemaineとMartin DemaineがQRコードとか折り紙に関する作品をいくつかデザインして展示しているとのことで,
本人の案内で見学に行きました.いろいろと刺激的で楽しい展示でした.
MITのErik DemaineとMartin DemaineがQRコードとか折り紙に関する作品をいくつかデザインして展示しているとのことで,
本人の案内で見学に行きました.いろいろと刺激的で楽しい展示でした.
 Kendall駅の前に移転しておしゃれになったMIT博物館.いつもMuseum Shopしか行きませんが...
今回はActivating Origamiを購入.
折り紙と折り図と回路が入っていて,振動させたり光らせたりできます.
折り紙を振動させたり光らせたりしてどうすんだとか言ってはいけません.
さすがMITっぽいものを売ってるなぁと思う次第.
Kendall駅の前に移転しておしゃれになったMIT博物館.いつもMuseum Shopしか行きませんが...
今回はActivating Origamiを購入.
折り紙と折り図と回路が入っていて,振動させたり光らせたりできます.
折り紙を振動させたり光らせたりしてどうすんだとか言ってはいけません.
さすがMITっぽいものを売ってるなぁと思う次第.
 BostonのグリーンラインのLechmere駅から歩いてすぐのところにあるアンティークショップ.地上4階地下1階に,
ぎっちりアンティークショップが入っていて,かなり楽しいです.以前は入場料がかかった覚えがあるけれど,
無料になっていました.駅近辺もすごく綺麗になっていて雰囲気が明るくなりました.
今回は以下の5つを購入.散財しました.
BostonのグリーンラインのLechmere駅から歩いてすぐのところにあるアンティークショップ.地上4階地下1階に,
ぎっちりアンティークショップが入っていて,かなり楽しいです.以前は入場料がかかった覚えがあるけれど,
無料になっていました.駅近辺もすごく綺麗になっていて雰囲気が明るくなりました.
今回は以下の5つを購入.散財しました.








 書籍:『完全版マーティン・ガードナー数学ゲーム全集』
書籍:『完全版マーティン・ガードナー数学ゲーム全集』

 書籍編集『ORIGAMI6』
書籍編集『ORIGAMI6』
 書籍:『はじめてのアルゴリズム』
書籍:『はじめてのアルゴリズム』
 書籍:『折り紙のすうり』
書籍:『折り紙のすうり』
 書籍:『ゲームとパズルの計算量』
書籍:『ゲームとパズルの計算量』
 書籍:『幾何的な折りアルゴリズム』
書籍:『幾何的な折りアルゴリズム』


